1、基本GAN及其缺陷

1.1、KL散度与JS散度

KL散度可衡量两个分布的距离：

$$D_{K L}(P \| Q)=\sum_{x \in X} P(x) \log \frac{P(x)}{Q(x)}$$

但KL散度不对称，将其中一个分布带入P和带入Q，得到的结果不同。JS散度对KL散度进行修正，保证了对称性：

$$J S(P \| Q)=\frac{1}{2} K L\left(P \| \frac{P+Q}{2}\right)+\frac{1}{2} K L\left(Q \| \frac{P+Q}{2}\right)$$

1.2、GAN LOSS

GAN LOSS的表达式为对真实样本与生成样本的交叉熵损失函数。设$P_{data}$为真实样本的分布，$x$ 为真实样本，$P_z$ 为随机噪声的分布，$z$ 为随机噪声，$P_G$ 为生成器所生成的样本分布，那么我们的目标是$P_G = P_{data}$。

$$\min _{G} \max _{D} V(D, G)=E_{x \sim p_{\text {data }}(x)}[\log D(x)]+E_{z \sim p_{z}(z)}[\log (1-D(G(z)))]$$

当判别器D在迭代优化时，其输入x，对判别的的loss的贡献为：

$$-P_{data}(x) \log D(x)-P_{G}(x) \log [1-D(x)]$$

我们可以求出判别器最优时的状态，即对上式中$D(x)$求导等于0，得出：

$$-\frac{P_{data}(x)}{D(x)}+\frac{P_{G}(x)}{1-D(x)}=0 \rightarrow D^{*}(x)=\frac{P_{data}(x)}{P_{data}(x)+P_{G}(x)}$$

此为最优判别器$D^{*}(x)$的表达式，也就是当生成器G生成效果足够好，$D^{*}(x)$难以区分真实图片与生成图片，即当$P_G=P_{data}$时，$D^{*}(x)=\frac{1}{2}$。

1.3、GAN LOSS的缺陷

GAN需要平衡判别器与生成器的训练。判别器往往更容易被训练的较好（因为判别器是分类任务，显而易见比生成器从噪声生成图片的任务要简单得多）。但过于准确的判别器会导致生成器学不到任何东西。当把最优判别器$D^{*}(x)$带入GAN LOSS中，得到：

$$\begin{aligned} V\left(D_{G}^{*}, G\right) &=\mathrm{E}_{x \sim P_{data}(x)}\left[\log D_{G}^{*}(x)\right]+\mathrm{E}_{x \sim P_{G}(x)}\left[\log \left(1-D_{G}^{*}(x)\right)\right] \\ &=\mathrm{E}_{x \sim P_{data}(x)}\left[\log \frac{P_{data}}{P_{data}+P_{G}}\right]+\mathrm{E}_{x \sim P_{G}(x)}\left[\log \left(1-\frac{P_{data}}{P_{data}+P_{G}}\right)\right] \\ &=-2\log 2+2 \mathrm{JS}\left(P_{data} \| P_{G}\right) \end{aligned}$$

即生成器的损失等价于真实分布与生成样本分布的JS散度。但JS散度只有在两个分布有重叠部分时才会生效，（原因：https://blog.csdn.net/Invokar/article/details/88917214 ）。如果两个分布没有重叠，那么JS散度无法给生成器提供梯度，生成器的损失函数值恒为$-2log2$，求导后为0。

事实上，两个分布大概率没有重叠部分：当$P_{data}$与$P_{G}$的支撑集（概率密度非0部分）是高维空间中的低维流形（manifold）时，$P_{data}$与$P_{G}$重叠部分测度（measure）为0的概率为1。$P_{G}$的支撑集是低维流形的原因是，整个图片虽然像素数很多，但其由N维的向量作为输入而得到。

---

2、WGAN与WGAN-GP

2.1、WGAN

WGAN使用另一种衡量分布距离的方式：Wasserstein距离。它能在两个分布完全没有重叠是也能衡量分布距离。Wasserstein距离的含义为推土机距离：一个分布代表土堆，另一个分布代表坑，求将土堆推入坑所消耗的成本即为推土机距离。（关于其数学表达参考 https://zhuanlan.zhihu.com/p/25071913 的第三部分）（题外话，推土机距离的离散形式也可以拿来做文章，某篇CVPR2021使用拉普拉斯金字塔做风格迁移的网络就是使用离散推土机距离做损失函数的）

根据某些理论，当判别器满足Lipschitz连续，即可使用判别器拟合Wasserstein距离。此时判别器的任务是：$\mathbb{E}_{x \sim P_{G(x)}}\left[D_{w}(x)\right]-\mathbb{E}_{x \sim P_{data}}\left[D_{w}(x)\right]$，而生成器的任务是减小生成样本与真实样本的Wasserstein距离：$-\mathbb{E}_{x \sim P_{g}}\left[f_{w}(x)\right]$。（真实样本部分对生成器无梯度，所以忽略）

此时判别器的改动有：

• 由真假样本的分类任务变为拟合Wasserstein距离的回归任务，取消sigmoid层。
• 生成器和判别器的loss不取log
• 每次更新判别器的参数之后把它们的绝对值截断到不超过一个固定常数c
• 不要用基于动量的优化算法（包括momentum和Adam）（经验之谈）

2.2、WGAN-GP

WGAN中暴力的将超过常数c的梯度截断，会导致三个问题，一是参数更新的方向被改变了，已经不是梯度的负方向了，二是梯度分布不均衡：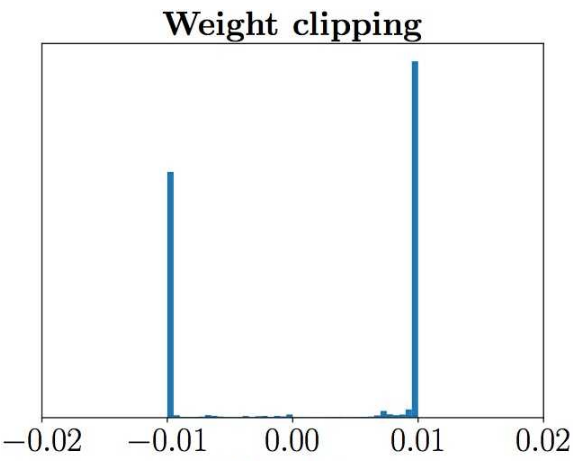
，

第三个问题是，这样暴力操作很容易导致梯度消失或爆炸。因为如果梯度偏小，连续的卷积带来更小的梯度。梯度偏大同理。导致调节截断位置很困难。

WGAN-GP不使用暴力的方式来约束梯度，而是作为loss中的一项，让判别器在训练的时候自己学习让网络的梯度在某一区间的网络参数。不过满足Lipschitz连续需要让网络对整个样本空间的任何输入都满足，实际上我们无法得到“任何输入”，所以一个折中方案是对真实样本与生成样本做插值，来得到多样化的样本来近似“任何输入”。

损失函数为：

$$L=\underbrace{\underset{\tilde{x} \sim \mathbb{P}_{G(x)}}{\mathbb{E}}[D(\tilde{x})]-\underset{x \sim \mathbb{P}_{data}}{\mathbb{E}}[D(\boldsymbol{x})]}_{\text {Original critic loss }}+\underbrace{\lambda \underset{\hat{\boldsymbol{x}} \sim \mathbb{P}_{\hat{\boldsymbol{x}}}}{\mathbb{E}}\left[\left(\left\|\nabla_{\hat{\boldsymbol{x}}} D(\hat{\boldsymbol{x}})\right\|_{2}-1\right)^{2}\right]}_{\text {Our gradient penalty }} .$$

其中：$\hat{\boldsymbol{x}} \leftarrow \epsilon \boldsymbol{x}+(1-\epsilon) \tilde{\boldsymbol{x}}$

3、Spectral Norm

3.1、原理

判别器D满足Lipschitz连续，当且仅当网络的每一层都满足Lipschitz连续。其中激活函数如ReLU，Leaky ReLU 等都满足该条件，那么为了让整个网络满足 Lipschitz 条件，只要对每个卷积层都进行约束即可。

卷积操作实际上就是矩阵乘法，而对于矩阵$W: R^{n} \rightarrow R^{m}$，K-Lipschitz 条件表示为：

$$\|Wx\| \leq K\|x\|, \forall x \in R^{n}$$

等价于：

$$\left\langle\left(W^{T} W-K^{2}\right) x, x\right\rangle \leq 0$$

设$W^TW$的特征值为$\lambda_i$，对应的特征向量构成的基底为$v_i$（对称矩阵的不同特征值的对应的特征向量正交），则可设$x=x_1v_1+x_2v_2+ \dots + x_nv_n$，
那么原式变为：

$$\begin{aligned} \left\langle\left(\mathrm{W}^{\mathrm{T}} \mathrm{W}-\mathrm{K}^{2}\right) \mathrm{x}, \mathrm{x}\right\rangle \leq 0 &=\left\langle\left(\mathrm{W}^{\mathrm{T}} \mathrm{W}-\mathrm{K}^{2}\right) \sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{x}_{\mathrm{i}} \mathrm{v}_{\mathrm{i}}, \sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{x}_{\mathrm{j}} \mathrm{v}_{\mathrm{j}}\right\rangle \\ &=\sum_{\mathrm{i}=1}^{\mathrm{n}} \sum_{\mathrm{j}=1}^{\mathrm{n}} \mathrm{x}_{\mathrm{i}} \mathrm{x}_{\mathrm{j}}\left\langle\left(\mathrm{W}^{\mathrm{T}} \mathrm{W}-\mathrm{K}^{2}\right) \mathrm{v}_{\mathrm{i}}, \mathrm{v}_{\mathrm{j}}\right\rangle \\ &=\sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\lambda_{\mathrm{i}}-\mathrm{K}^{2}\right) \mathrm{x}_{\mathrm{i}}^{2} \leq 0 \\ & \Rightarrow \sum_{\mathrm{i}=1}^{\mathrm{n}}\left(\mathrm{K}^{2}-\lambda_{\mathrm{i}}\right) \mathrm{x}_{\mathrm{i}}^{2} \geq 0 \end{aligned}$$

若要使该式恒成立，需要使$K^2$大于最大的$\lambda_1$，即使矩阵 $W$ 的最大奇异值$\sqrt{\lambda_1}$小于 K。那么只需要对矩阵$W$中的每个元素都除以$W$的最大奇异值$\sqrt{\lambda_1}$，即可满足该层满足1-Lipschitz 条件

3.2、实现

在前向传播中，每次求解卷积层的最大奇异值时间复杂度太高，于是可以使用幂迭代法求解，先求解最大奇异值对应的奇异向量：

$$\begin{aligned} \tilde{v} &:=\frac{W^{T} \tilde{u}}{\left\|W^{T} \tilde{u}\right\|_{2}} \\ \tilde{u} &:=\frac{W \tilde{v}}{\|W \tilde{v}\|_{2}} \end{aligned}$$

得到最大奇异值：

$$\begin{aligned} &W^{T} W \tilde{v}=\lambda_{1} v,\|v\|_{2}=1 \\ &\Rightarrow \tilde{v}^{T} W^{T} W \tilde{v}=\lambda_{1} v^{T} v=\lambda_{1} \\ &\Rightarrow\langle W \tilde{v}, W \tilde{v}\rangle=\lambda_{1} \\ &\Rightarrow\|W \tilde{v}\|_{2}=\sqrt{\lambda_{1}} \end{aligned}$$

那么使用上述的第二个迭代式子两边同时乘以$\tilde{u}^T$，即可使用$\tilde{v}$和$\tilde{u}$计算$\lambda_{1}$:

$$\begin{aligned} \tilde{u}^{T} \tilde{u} &=\frac{\tilde{u}^{T} W \tilde{v}}{\|W \tilde{v}\|_{2}} \\ 1 &=\frac{\tilde{u}^{T} W \tilde{v}}{\sqrt{\lambda_{1}}} \\ \sqrt{\lambda_{1}} &=\tilde{u}^{T} W \tilde{v} \end{aligned}$$

---

4、其他GAN loss

待补充：

• LSGAN
• hinge loss

---

5、 GAN的评价指标

5.1、IS (Inception Score)

将生成图片送入已经训练好Inception-v3模型，会得到一个1000维的向量，代表图片属于每一类别的概率。若生成图片质量够高，那么其会以很高的概率被分到某一个类，所以可以使用概率向量的熵来代表概率分布的混乱程度：

$$H(y|x)=-\sum_{i=1} p\left(y_{i} \mid x\right) \log \left[p\left(y_{i} \mid x\right)\right]$$

同时希望GAN能够生成多样化的样本，即不同类别的生成样本数量近似相等。可以对全部样本的输出的概率密度做平均来代表全部样本的类别分布：

$$\frac{1}{N} \sum_{i=1}^{N} p\left(y \mid x_{i}\right) \approx \mathbb{E}_{x}[p(y \mid x)]=p(y)$$

那么同样使用熵来代表混乱程度：

$$H(y)=-\sum_{i=1}^{n} p\left(y_{i}\right) \log \left[p\left(y_{i}\right)\right]$$

好的GAN应该为：不考虑x时的边缘分布$H(y)$高，代表其不确定性高，在得到确定的生成图片x后，其概率的熵$H(y|x)$低，即：

$$\mathbb{E}_{x}\left[D_{K L}(p(y \mid x) \| p(y))\right]=H(y)-H(y \mid x)$$

差值越大越好。为了便于计算与比较，对上式添加指数：

$$IS = \exp \left(\frac{1}{N} \sum_{i=1}^{N} D_{K L}\left(p\left(y \mid x^{(i)}\right) \| \hat{p}(y)\right)\right)$$

5.1.1、缺点

• 当GAN发生过拟合时，生成器只“记住了”训练集的样本，由于样本质量和多样性都比较好，IS仍然会很高。
• Inception Net-V3是在ImageNet上训练得到的，所以如果训练集图片不在ImageNet的类别中，IS值也会很低。
• 无法检测类内模式崩溃

5.2、FID(Fréchet Inception Distance)

分别把生成器生成的样本和判别器生成的样本送到分类器中（例如Inception Net-V3或者其他CNN等），抽取分类器的中间层的抽象特征，并假设该抽象特征符合多元高斯分布，估计生成样本高斯分布的均值 $\mu_g$ 和方差 $\Sigma_g$ ，以及训练样本 $\mu_{data}$ 和方差 $\Sigma_{data}$ ，计算两个高斯分布的弗雷歇距离，此距离值即FID:

$$FID = \left\|\mu_{\text {data }}-\mu_{g}\right\|+\operatorname{tr}\left(\Sigma_{\text {data }}+\Sigma_{g}-2\left(\Sigma_{\text {data }} \Sigma_{g}\right)^{\frac{1}{2}}\right)$$

越小越好

5.2.1、缺点

FID和IS都是基于特征提取，也就是依赖于某些特征的出现或者不出现。但是他们都无法描述这些特征的空间关系。（假如图片中嘴在眼睛上方是一个失败的生成样本，但FID会很高）

---

6、各种GAN

待补充

• PatchGAN、SinGAN（特殊判别器）
• ProgressiveGAN、MSG-GAN（高分辨率生成）
• GauGAN（主要引出六种Norm）
• StyleGAN v1v2 （和v3？）
• StarGAN v1v2
• VQGAN（transformer）

---

7、参考

https://zhuanlan.zhihu.com/p/25071913
https://www.zhihu.com/question/52602529/answer/158727900
https://blog.csdn.net/weixin_41036461/article/details/82385334
https://blog.csdn.net/StreamRock/article/details/83590347
https://www.sohu.com/a/294399864_500659
https://zhuanlan.zhihu.com/p/109342043
https://blog.csdn.net/qq_27261889/article/details/86483505